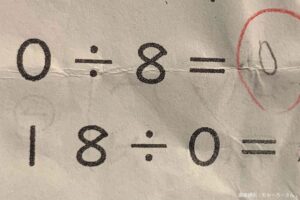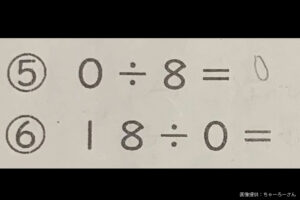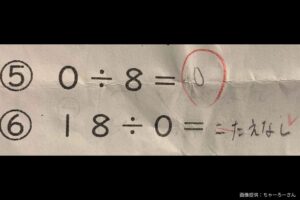小3娘の宿題、担任の採点が酷すぎると話題に　文科省は「小学校で指導しない範囲」認める

 

 

■文科省は「存在しません」と断言

数字を0で割る、いわゆる「ゼロ除算」について、文部科学省・教育課程課の担当者は「学習指導要領に載っていない内容となります」「つまり、小学校の算数教育において『数字を0で割る』指導は、前提として存在しません」と、説明する。

児童の算数教育の話題で、定期的に波紋を呼んでいるのが「超算数」と呼ばれる問題。

こちらは、かけ算（乗法）の文章問題における「答えが合っていても、式に登場する数字の順番が異なればバツ（良くて三角）」というもので、小学2年生の児童らにトラウマ級の辛酸を舐めさせている。

授業中に「式内の数字の順番」の重要性について指導する教員もいるようだが、中には「テストの採点後に初めてこのルールを明かす」教員も少なくないようで、古来より児童はもちろん、保護者に忌み嫌われてきた。

X上でもしばしば、こちらの「超算数」に関する疑問の投稿が大きな話題を呼び、記者も文科省に取材を実施したことが。

下手をすると「悪問」にカテゴライズされる内容だが、こちらは少なくとも「小学校学習指導要領」における「第2学年の内容」の「A 数と計算」の項に登場し、文科省は「ここで述べた被乗数と乗数の順序は、『一つ分の大きさの幾つ分かに当たる大きさを求める』という日常生活などの問題の場面を式で表現する場合に大切にすべきことである」と言及している。

ただし、テスト等で実際に「丸にするか、バツをつけるか」という判断は現場の裁量に委ねられており、いわば「担任教師ガチャ」のようになっているのが現状なのだ。

話を「ゼロ除算」に戻すと、こちらは学習指導要領に掲載されていない内容。つまり、日本史の授業における「武田信玄軍から敗走した徳川家康が、尻の汚れを『これは味噌だ』と主張した」といった雑学的なこぼれ話と、立場的には変わらないのである。

関連記事：『ジョブチューン』全品合格で出演シェフが…　“台本”について告白し反響呼ぶ

 

 

■数学のプロに見解を聞くと…

前出のような背景があり、そもそも小学校の算数の宿題（テスト）にゼロ除算が登場すること自体、おかしな話。しかし、反対に「数字を0で割ったらどうなるの？」という疑問を自ら教員にぶつける、好奇心旺盛な児童も少なくないだろう。

そこで続いては、数多くの生徒たちを合格に導いてきた『あすなろ学院』数学科・森山昇平氏に、「18÷0」の考え方を解説してもらうことに。

森山氏はまず、「私たちが普段行っている計算というのは『結果がいつでも1つに決まるからできる』というルールがあります」と説明する。

これは、例えば100円の飴󠄀と250円のグミを1つずつ買えば『100円＋250円＝350円』という数式が必要となり、言うなればいつでも「100＋250＝350」が成り立つため、支払う金額も1つ（350円）に決まるワケだ。

こちらの法則に注目し、森山氏は「逆に言えば『結果がいつでも1つに決まらない計算はできない』ということになります」と強調する。この性質と割り算の特徴を理解するには、割り算は「かけ算の逆の計算」であることを理解する必要があるのだ。

例えば、式「●÷0＝□」は式「□×0＝●」と同じ意味になる。このかけ算の左辺「□×0」に、様々な数を当てはめて計算してみよう。

□に1を当てはめると「1×0＝0」、□に2を当てはめると「2×0＝0」、□に4/3を当てはめると「4/3×0＝0」、□に0.567を当てはめると「0.567×0＝0」といったように、□に当てはまるのがどのような数だとしても、「□×0」は必ず0になる。

では、これらの式を「同じ意味の割り算」に変換すると、どうなるだろうか？

前出の法則の通り変換すると、かけ算「□×0＝0」は、割り算「0÷0＝□」となる。こちらに先ほど同様、数字を当てはめてみよう。

まず□に1を当てはめると「1×0＝0」なので「0÷0＝1」、□に2を当てはめると「2×0＝0」なので「0÷0＝2」、□に4/3を当てはめると「4/3×0＝0　」なので「0÷0＝4/3」、□に0.567を当てはめると「0.567×0＝0」なので「0÷0＝0.567」となる。

お分かり頂けただろうか…。「□×0＝0」のため、□に当てはまる数がどのような数でも「0÷0＝□」が成り立ってしまうのだ。

森山氏は「なんと『0÷0』の計算結果は、なんでもアリなのです！」「こうなってしまうと『0÷0』の計算結果で、何を書けば良いのか分からないですよね…。そのため『「0÷0」の計算結果は1つに決まらない』という意味で、『0÷0』は計算できません」と、補足している。

では、今回話題となった「18÷0」のように、「0でない数字」を0で割った場合は、どうなのだろうか。

こちらも割り算「（0でない数）÷0＝□」を、かけ算にすると「□×0＝（0でない数）」。しかし前出の通り、数字に0をかけると答えは0になるため、答えを「0でない数」とするのは不可能である。

つまり、まとめると…

（１）「0÷0」の計算結果はなんでもアリ。計算結果を「1つに決められない」ため、計算不可

（２）「（0でない数）÷0」の計算結果は「存在しない」ため、計算不可

となり、これらの事実から「数字を0で割る」計算は不可能なのだ。つまり今回のケースは、ちゃーろーさんの娘が回答した「こたえなし」が正解となる。

では、担任の指導通り「数字を0で割ると0になる」と認識してしまった場合、どのような弊害が考えられるのだろうか…。